Discussion Session 2

Grammar

  • Nonterminal
  • Terminal
  • Production Rule (Left Hand Side, Right Hand Side)

Example

start ::=  exp            // Start
exp   ::=  exp + term   // Add
exp   ::=  exp - term   // Minus
exp   ::=  term           // Term
term  ::=  ID              // Id
term  ::=  NUM             // Num
term  ::=  (exp)         // Group

Parsing

Parsing is the procedure of transforming a list of tokens into a tree with tokens as leaves.

Note

This process is also called derivation.

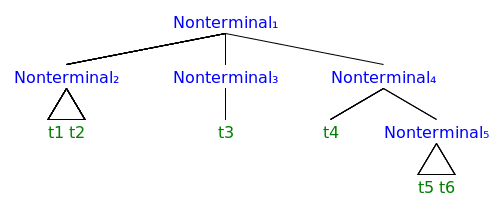
../../_images/syntax_tree012.png

Token stream t1, t2, t3, t4, t5, t6, ...... and Parsing Tree (Abstract Syntax)

Color Meaning
Green Terminal
Blue Nonterminal

Example

The abstract syntax for 1 - 2 - 3 - 4 goes as follows:

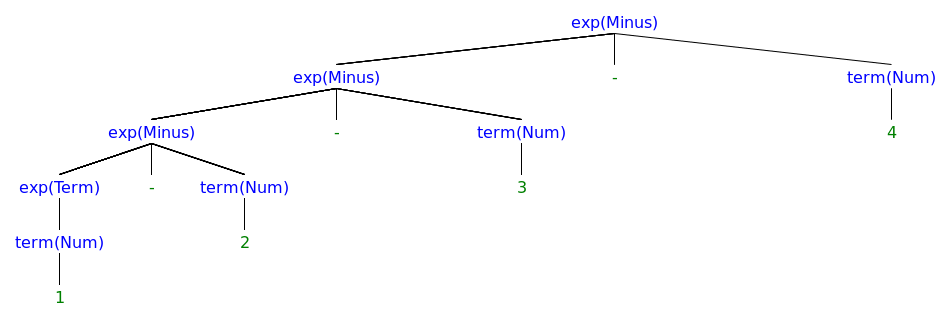
../../_images/parsing011.png

  • A good grammar has no ambiguity. Only one tree can be constructed from the token stream.

  • A good grammar should match human expectation.

    Example

    Try the following grammar on 1 - 2 - 3 - 4.

    start ::=  exp           // Start
exp   ::=  term + exp    // Add
exp   ::=  term - exp    // Minus
exp   ::=  term            // Term
term  ::=  ID               // Id
term  ::=  NUM              // Num
term  ::=  (exp)          // Group

Anatomy of LL(k)

L: Left-to-right

Examine the input (token stream) left-to-right in one parse.

L: Leftmost-derivation

Create / expand the left most sub-tree first.

Note

R: Rightmost-derivation

demo

Try parsing “1 + 2 - 3 * 4 + 5” with the following grammar.

start ::=  exp            // Start
exp   ::=  exp + term   // Add
exp   ::=  exp - term   // Minus
exp   ::=  term           // Term
term  ::=  term * NUM    // Mul
term  ::=  term / NUM    // Div
term  ::=  NUM             // Num
term  ::=  (exp)         // Group
../../_images/lr_step011.png

Step 1

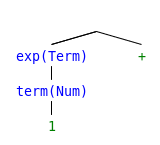
../../_images/lr_step021.png

Step 2

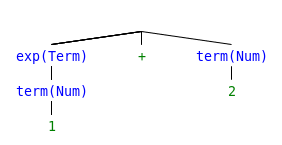
../../_images/lr_step031.png

Step 3

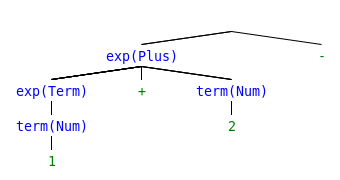
../../_images/lr_step041.png

Step 4

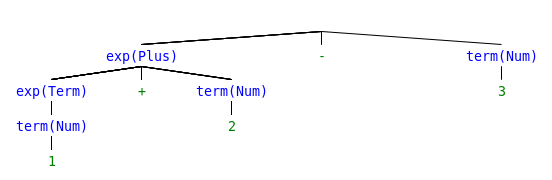
../../_images/lr_step051.png

Step 5

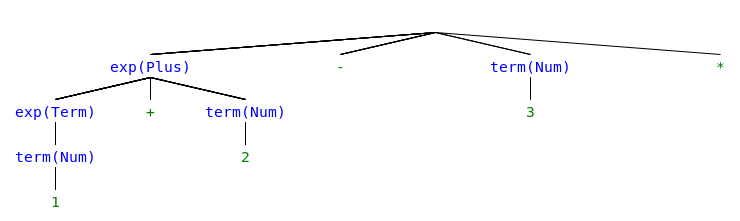
../../_images/lr_step061.png

Step 6

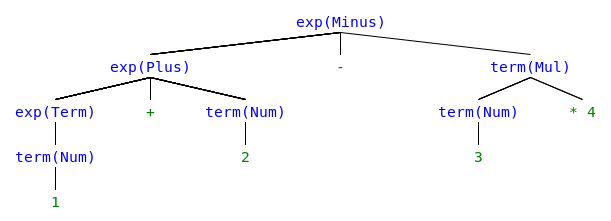
../../_images/lr_step071.png

Step 7

k: Lookahead

Inspect the first k tokens before making decision.

Eliminating Left Recursion

For productions like this:

\[P \rightarrow P\alpha_1 \mid P\alpha_2 \mid \cdots \mid P\alpha_m \mid \beta_1 \mid \cdots \mid \beta_n\]\[\textrm{where } \alpha \neq \varepsilon, \beta \textrm{ don't start with } P\]

It will be turned into

\[P \rightarrow \beta_1 P' \mid \beta_2 P' \mid \cdots \mid \beta_n P'\]\[P' \rightarrow \alpha_1 P' \mid \alpha_2 P' \mid \cdots \mid \alpha_m P' \mid \varepsilon\]

And you can verify that the resulting language is the same.

Warning

This is actually eliminating direct left recursions, and turning them into right recursions. There are methods to eliminate all recursions, direct or indirect, but it is more complicated, and needs some restrictions on the input grammar.

Example

start ::=  exp            // Start
exp   ::=  exp + term   // Add
exp   ::=  exp - term   // Minus
exp   ::=  term           // Term
term  ::=  ID              // Id
term  ::=  NUM             // Num
term  ::=  (exp)         // Group

is turned into

start ::=  exp
exp   ::=  term exp1
exp1  ::=  + term exp1
exp1  ::=  - term exp1
exp1  ::=  epsilon

Coding Demo

Left-factoring

For productions like this:

\[A \rightarrow \delta\beta_1 \mid \delta\beta_2 \mid\cdots\mid\delta\beta_n \mid \gamma_1 \mid \cdots \mid \gamma_m\]

We turn them into

\[A \rightarrow \delta A' \mid \gamma_1 \mid \cdots \mid \gamma_m\]\[A' \rightarrow \beta_1 \mid \cdots \mid \beta_n\]

Example

start ::=  exp          // Start
exp   ::=  exp + term   // Add
exp   ::=  exp - term   // Minus
exp   ::=  term           // Term
term  ::=  ID              // Id
term  ::=  NUM             // Num
term  ::=  (exp)         // Group

is turned into

start ::=  exp
exp   ::=  exp term1
term1 ::=  + term
term1 ::=  - term
exp   ::=  term

Do left recursion elimination.

start ::=  exp
exp   ::=  term exp1
exp1  ::=  term1 exp1
exp1  ::=  epsilon
term1 ::=  + term
term1 ::=  - term